Per gestire le tolleranze di progetto con lo scopo di avere prodotti che garantiscano determinati livelli di qualità a costi contenuti (idealmente per massimizzare i margini di guadagno) ci si basa sulla metodologia del Dimensional Management. Tale metodologia si avvale tra gli altri di due strumenti imprescindibili.
Il primo è rappresentato da una specifica geometrica di prodotto univoca. Essa si ottiene adottando un linguaggio tecnico universalmente riconosciuto e normato. Quello che in gergo comune è meglio noto con l’acronimo GD&T (Geometric Dimensioning & Tolerancing).
Il secondo strumento è rappresentato dai calcoli di catene di tolleranze (detta anche analisi delle tolleranze). Le approfondiamo in questo articolo.
Le catene di tolleranze
Questa attività di calcolo (troppo spesso trascurata per negligenza o incompetenza) è di fondamentale importanza per validare il proprio progetto dal punto di vista della propagazione delle tolleranze.
Con le catene delle tolleranze è possibile valutare infatti il rischio di interferenze durante le fasi di assemblaggio e/o il rispetto di distanze funzionali, che possono avere diversi scopi finali: garantire una determinata efficienza fluidodinamica, un determinato livello di campo elettro-magnetico, la tenuta di una guarnizione, ecc… dipendentemente dalla singola applicazione. Tali distanze sono identificate con il loro valore nominale (CAD) a progetto.
Sappiamo però che nel mondo reale (a causa dell’intrinseca imperfezione dei processi produttivi) il nominale non sarà mai perfettamente rispettato. E’ inevitabile che esso subisca delle variazioni. Tali variazioni sono causate dalle tolleranze. E in quest’ottica è fondamentale capire se le tolleranze a disegno possono causare la variazione del nominale oltre a dei limiti prefissati.
Superare tali limiti può compromettere in modo irreparabile il livello qualitativo di un prodotto oppure tale livello può essere successivamente recuperato solo attraverso delle correzioni (gestione delle non-conformità) che possono avere costi molto elevati. I risultati finali che si ottengono con questa attività di calcolo sono:
- Un progetto che “sulla carta” è funzionale (garantisce la qualità finale del prodotto),
- A disegno le tolleranze sono in numero minimo e indispensabile a garantire tale qualità e il loro valore (ampiezza della zona di tolleranza) è massimizzato. Quali sono le ripercussioni? Meno lavoro per produzione e qualità, maggiore produttività (potenziali processi produttivi “meno precisi”), minor rischio di avere scarti di produzione.
I calcoli di catene delle tolleranze vanno idealmente fatti prima di “congelare” il progetto e dell’emissione dei disegni tecnici verso la produzione.
Perché?
Non esiste motivazione più semplice: accorgersi di potenziali problemi qualitativi causati dalle tolleranze e risolverli prima di industrializzare il prodotto ha dei costi che sono di qualche ordine di grandezza inferiori rispetto a rilevare lo stesso problema in linea di assemblaggio quando:
- Gli stampi e/o le attrezzature sono già state costruite
- La produzione realizzata e i componenti spediti dai fornitori sparsi in giro per il mondo
- I controlli qualità effettuati con tutti i relativi costi annessi
I calcoli di catene delle tolleranze dovrebbero essere i “migliori amici” di ogni titolare o amministratore di azienda che sviluppa prodotti e dovrebbero essere inseriti in modo imprescindibile all’interno del processo di sviluppo stesso.
Figura 1. La costante necessità da parte delle aziende di bilanciare le performance
sul prodotto con i costi di produzione dello stesso.
Il calcolo delle catene di tolleranze
Dal punto di vista pratico l’analisi delle tolleranze può essere fatta con metodi differenti. I due metodi più diffusi sono:
- Approccio “worst case”,
- Approccio statistico.
Mettiamoli a confronto per sottolineare loro pregi e difetti.
Approccio "worst case"
Il worst case è l’approccio con cui tradizionalmente si è iniziato ad affrontare questa tipologia di calcoli. Questo perché è un metodo che ben si adatta a calcoli manuali o al più supportati da fogli di calcolo, semplici ed economici.
Questo approccio è utilizzato quando le catene sono realizzate da tolleranze dimensionali mentre diventa macchinoso quando sono presenti nello schema di quotatura delle tolleranze geometriche. Le variabili (tolleranze) sono considerate solo ai loro valori limiti di specifica; il risultato che si ottiene è caratterizzato da valori massimo e minimo che ne definiscono la potenziale variabilità. Vediamone un esempio:
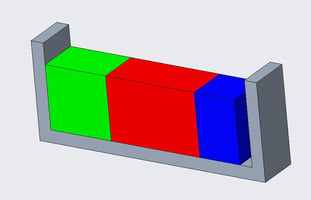
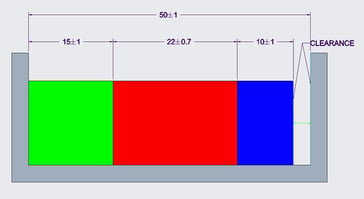
Figura 2. Esempio di catena delle tolleranze lineare (monodimensionale).
Ipotizziamo di dover inserire i tre prismi verde, rosso e blu nel loro alloggiamento. Per garantire la loro assemblabilità è necessario che la distanza “clearance” sia sempre positiva. Il suo valore nominale è 50 - 15 - 22 - 10 = 3mm. Tale valore è soggetto a variazione a causa delle tolleranze. Prevedere tale variazione con un calcolo worst case significa valutare la massima e minima “clearance” possibili. In particolare:
- La clearance massima si verifica al massimo della larghezza della sede (51 mm) e al minimo della larghezza dei tre prismi (14, 21.3 e 9 mm rispettivamente). "max clearance" = 51 - 14 - 21.3 - 9 = 6.7mm
- La clearance minima si verifica al minimo della larghezza della sede (49 mm) e al massimo della larghezza dei tre prismi (16, 22.7 e 11 mm rispettivamente). "min clearance" = 49 - 16 - 22.7 - 11 = -0.7mm
Figura 3. Previsione di variabilità associata alla clearence definita in Fig.2 e in
funzione della catena di tolleranze espressa nella figura stessa.
Il calcolo prevede per la clearance minima un valore negativo (-0.7 mm), che si traduce nella pratica come possibile interferenza e quindi impossibilità a garantire l’assemblaggio. Per ristabilire tale condizione è necessario stringere le tolleranze di 0.7 mm totali, valore da ripartire tra le quattro quote della catena.
Progettare con approccio worst case garantisce la funzionalità del 100% dei prodotti ed è usato quando non sono assolutamente ammessi potenziali failure (dispositivi salvavita, satelliti, ecc…). Il suo principale svantaggio deriva dall’utilizzo di tolleranze che nella maggior parte dei casi sono troppo cautelative per le reali esigenze del prodotto.
Questo accade perché si presume che le varie quote della catena siano tutte e contemporaneamente prodotte al limite inferiore oppure al limite superiore di specifica, quando invece l’obiettivo di processo è quello di avvicinarsi al nominale di ogni singola quota. E’ tutta una questione di probabilità: qual è la possibilità, nel mondo reale, che tutte le quote della catena siano prodotte contemporaneamente al loro limite inferiore (o superiore) di specifica?
La risposta è che questa probabilità è molto (troppo?) bassa e tende a diminuire con l’aumentare della lunghezza della catena di tolleranze. Questo comporta come conseguenza alti costi di produzione per ottenere le precisioni richieste o alto numero di scarti(e quindi alti costi, due facce della stessa medaglia), non tanto per una reale necessità ma a causa di un metodo di calcolo inadeguato nel fornire una previsione statisticamente affidabile.
Approccio statistico
Per superare queste limitazioni si utilizza l’approccio statistico. Tale metodo di calcolo implica di assegnare ad ogni variabile una distribuzione statistica in modo da avere una maggiore probabilità associata al valore nominale rispetto ai valori di estremità del campo di tolleranza:
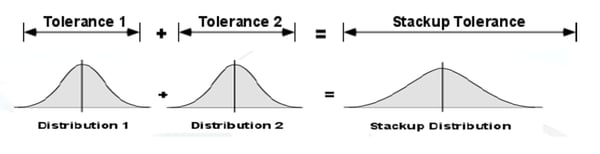Figura 4. Confronto tra approccio "worst case" e approccio "statistico" nella definizione delle variabili
nelle catene delle tolleranze. Da sottolineare che l'altezza della distribuzione statistica è
rappresentativa delle probabilità di ottenere un determinato valore della quota.
Ricalcolando la stessa catena di tolleranze della Fig. 2 con l’approccio statistico si ottiene il risultato di Fig. 5: la variabilità è ora rappresentata da una distribuzione statistica (curva gaussiana) il cui valore medio (valore associato con la massima probabilità) è di 3 mm. Dal punto di vista matematico la curva gaussiana ha le code infinitamente lunghe, ed è quindi illimitata.
Con lo scopo di definire una variabilità da associare alla clearance si introduce un criterio di troncamento della curva. In questo caso la curva è stata troncata a ± tre volte il valore della deviazione standard (0.62272 mm è il valore numerico che quantifica la dispersione della distribuzione attorno al suo valore medio).
Questo criterio di troncamento implica un livello di affidabilità del 99.73%.
Figura 5. Confronto tra la variabilità associata alla clearance prevista con
approccio worst case e con approccio statistico.
E’ quindi possibile concludere che la variabilità totale associata clearance è quella riportata dai valori all’interno dei rettangoli verdi di Fig. 5 (con una livello di confidenza del 99.73%). In particolare la previsione della clearence minima riporta un valore positivo di 1.132 mm. Tale valore è da confrontare con la previsione fatta con l’approccio worst case per la medesima catena delle tolleranze (-0.7 mm).
Le ripercussioni sono rilevanti: mentre il calcolo con approccio worst case impone di stringere le tolleranze per garantire l’assemblabilità lo stesso calcolo, fatto con approccio statistico, permette addirittura un loro allargamento essendoci un margine rilevante tra il valore minimo della clearence (1.132 mm) e il suo limite funzionale (0.000 mm). Portando ad esempio le tolleranze ai seguenti valori:
- 15 ± 1.5 mm (+50%),
- 22.0 ± 1.4 mm (+100%),
- 10.0 ± 1.5 mm (+50%),
il risultato che si ottiene è riportato nella seguente figura; anche con le tolleranze allargate l’assemblabilità è garantita!
Figura 6. Ricalcolo della clearence con entrambi gli approcci worst case e statistico a seguito
dell’allargamento del campo di tolleranze associate alle larghezza dei prismi verde, rosso e blu.
1D vs 3D
Oltre a quanto detto fino a questo momento aggiungiamo inoltre che l’approccio worst case è applicato quasi esclusivamente a catene semplificate monodimensionali, unico modo per rendere l’analisi delle tolleranze fattibile manualmente con tempistiche compatibili con i tempi di sviluppo industriali. Questa semplificazione si scontra con la realtà sempre tridimensionale dei prodotti.
Simulando infatti una catena delle tolleranze 1D il rischio è quello di sottostimare la variabilità reale delle distanze funzionali che si sta considerando. Questo avviene in quanto nel 3D le tolleranze subiscono degli effetti di amplificazione che il calcolo monodimensionale non può rilevare:
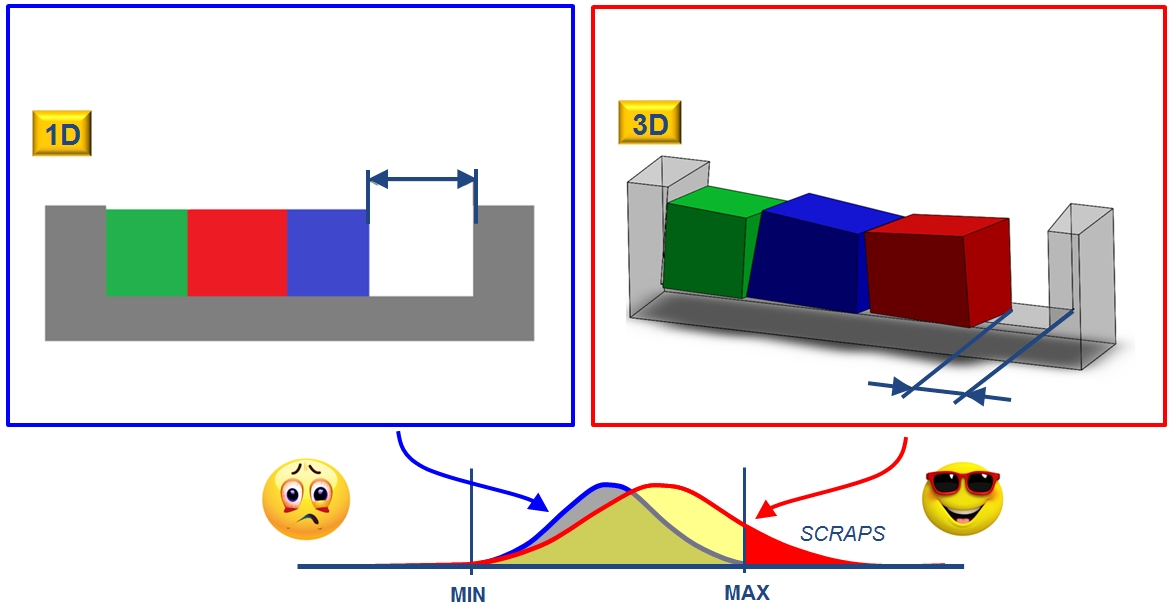
Figura 7. Contributo della tridimensionalità dei modelli di calcolo all’affidabilità
dei risultati derivanti da analisi delle tolleranze.
Gli effetti di amplificazione sono causati dall’interazione con tra l’ampiezza della zone di tolleranza e la dimensione nominale delle feature geometriche sulle quali esse sono applicate. A parità di zona di tolleranza, maggiore è l’estensione nominale della feature e minori saranno le variabilità angolari ad esse concesse. Il calcolo 1D non è in grado di prendere in considerazione tali effetti.
Il rischio è quindi di stimare con il calcolo 1D delle variazioni in “svantaggio di sicurezza” con la conseguenza di rendere queste previsioni poco utili, in quanto molto poco affidabili (che sia proprio questo uno dei motivi, assieme al worst case, per cui lo scetticismo sull’analisi delle tolleranze è ancora molto diffuso?).
Il ruolo della simulazione
Il principale “svantaggio” dei calcoli di catene delle tolleranze 3D con approccio statistico è rappresentato dalla loro complessità, che li rende impraticabili dal punto di vista manuale.
Fortunatamente sono disponibili software di simulazione dedicati a gestire questa complessità matematica che permettono al progettista di svolgere calcoli molto complessi in modo agevole e in tempi molto contenuti. Tali modelli di calcolo sono costruiti a partire dal CAD 3D nominale del prodotto sul quale vengono definite le varie tolleranze e i requisiti da calcolare, il tutto con interfaccia e strumenti dedicati all’attività.
I vantaggi della simulazione rispetto al calcolo worst case monodimensionale possono essere quindi riassunti:
- Modelli 3D rispetto alla semplificazione 1D,
- Possibilità di considerare sia le tolleranze geometriche che quelle dimensionali. Nel calcolo 1D worst case le tolleranze geometriche sono molto difficili da gestire,
- Possibilità di gestire un numero di quote tolleranze potenzialmente illimitato,
- Tempi di costruzione del modello di calcolo irrisori in confronto al calcolo manuale,
- Strumenti avanzati per comprendere e mettere in pratica le migliori azioni correttive nel bilanciamento tra costi e benefici,
- Pochi input manuali soggetti ad errori di distrazione.
Il vantaggio principale resta però legato all’elevata affidabilità dei risultati derivanti dal calcolo. Se ti interessa saperne di più su queste tecniche per scoprire come applicarle al vostro processo di progettazione contattaci, uno dei nostri esperti risponderà a tutte le tue domande.
